+ 86-18052080815 | info@harsle.com
Vistas:138 Autor:Editor del sitio Hora de publicación: 2024-08-30 Origen:Sitio
Calcular el diseño correcto del plano es crucial para obtener una pieza terminada de buena calidad de su prensa plegadora. Sin embargo, muchos programadores de CAD y CNC no tienen idea de cómo calcular los valores requeridos. Hace años, los verdaderos expertos crearon hojas de referencia y las clavaron en la pared. Solo le enseñaron al nuevo aprendiz cómo aplicar los resultados que se muestran en la hoja de trucos, no cómo calcular los números. Bueno, ahora esos expertos se han retirado y es hora de que una nueva generación aprenda la forma correcta de calcular el diseño de desarrollo correcto.
Calcular la longitud del patrón plano a partir de la pieza 3D realmente no es tan difícil. Aunque puede encontrar varias fórmulas diferentes que afirman calcular el margen de curvatura (Consulte Definiciones de flexión), por lo general tienen la misma fórmula, solo que simplificada al completar el ángulo o un factor K. Ah, y sí, es necesario conocer el factor K para calcular el margen de flexión.

Comencemos con un soporte en L simple. La imagen muestra que las patas del soporte son de 2' y 3'. El espesor del material es 0,125', el radio interior es 0,250' y el ángulo de curvatura es 90 grados. La longitud plana es el total de la porción plana de ambas bridas más la longitud a través del arco del área de curvatura. Pero, ¿calculas eso por dentro del material o por fuera? ¡Ni! Aquí es donde entra en juego el factor K. El factor K es el porcentaje del espesor del material donde no hay estiramiento ni compresión del material, por ejemplo, el eje neutro. Para este soporte en L simple, usaré un factor K de 0,42.

La fórmula (ver Fórmulas de flexión) es:
Margen de curvatura = Ángulo * (π / 180) * (Radio + Factor K * Espesor).
Al ingresar nuestros números, tenemos: Margen de flexión = 90 * (π / 180) * (0,250 + 0,42 * 0,125) = 0,475'
Entonces, la longitud del patrón plano es 1.625' + 2.625' + 0.475' que es igual a 4.725'. Entonces, si suma la longitud plana de todas las bridas y agrega un margen de curvatura para cada área de curvatura, tendrá la longitud plana correcta de la pieza.
Pero mira el dibujo. Normalmente no dimensionamos así una pieza de chapa. Las dimensiones suelen ser hasta la intersección de las bridas o la línea del molde. Esto significa que tenemos que restar dos veces el espesor del material más el radio de curvatura (también conocido como retroceso) para cada área de curvatura. Para este conjunto de dimensiones, sería más fácil calcular el valor de Compensación de pliegue. El valor de Compensación de pliegue le permite sumar la longitud de cada pestaña usando las dimensiones de la Línea de molde y luego agregar una Compensación de pliegue por área de pliegue al total. Es -0,275, un número negativo, lo que significa que restarás esta cantidad del total de las longitudes de las bridas, 5', para obtener 4,725'.
Margen de curvatura = Ángulo * (π / 180) * (Radio + Factor K * Espesor)
Compensación de curvatura = Margen de curvatura – (2 * Retroceso)
Retroceso interior = bronceado (ángulo / 2) * radio exterior
Retroceso = bronceado (Ángulo / 2) * (Radio + Espesor)

Tolerancia de curvatura – La longitud del arco que pasa por el área de pliegue en el eje neutro.
Ángulo de curvatura – El ángulo incluido del arco formado por la operación de flexión.
Compensación de curvatura – La cantidad en la que el material se estira o comprime mediante la operación de doblado. Se supone que todo estiramiento o compresión ocurre en el área de flexión.
Líneas de curvatura – Las líneas rectas en las superficies interior y exterior del material donde el límite de la brida se encuentra con el área de curvatura.
Radio de curvatura interior – El radio del arco en la superficie interior del área de plegado.
factor K – Define la ubicación del eje neutro. Se mide como la distancia desde el interior del material hasta el eje neutro dividida por el espesor del material.
Líneas de molde – Para curvas de menos de 180 grados, las líneas del molde son las líneas rectas donde se cruzan las superficies de la brida que limitan el área de curvatura. Esto ocurre tanto en las superficies interior como exterior de la curva.
Eje neutro – Mirando la sección transversal de la curvatura, el eje neutro es el lugar teórico en el que el material no se comprime ni se estira.
Retrasar - Para curvas de menos de 180 grados, el retroceso es la distancia desde las líneas de curvatura hasta la línea del molde.
Que yo sepa, no existe una fórmula para calcular el factor k. Oh, estoy seguro de que algún ingeniero matemático tiene una fórmula en algún lugar. Pero lo más probable es que sea demasiado complejo para que la mayoría de nosotros lo comprendamos o podamos utilizar.
El factor k es el porcentaje del espesor del material donde no hay estiramiento ni compresión del material en el área de flexión. ¡Así, el eje neutro!
Cuanto más duro es el material, menos compresión hay en el interior de la curva. Por lo tanto, se estira más en el exterior y el eje neutro se mueve hacia el interior de la curva. Los materiales más blandos permiten una mayor compresión en el interior y el eje neutro permanece más cerca del centro del espesor del material.
El radio de curvatura tiene un efecto similar. Cuanto menor sea el radio de curvatura, mayor será la necesidad de compresión y el eje neutro se moverá hacia el interior de la curvatura. En un radio mayor. el eje neutro permanece cerca del centro del espesor del material.

Para ayudarlo a dominar la fórmula de cálculo de la longitud de flexión desplegada de manera más simple y rápida, enumeramos cuatro tablas de coeficientes comunes, ilustramos dieciséis fórmulas de cálculo de la longitud de flexión desplegada y también tomamos algunos ejemplos para una mejor comprensión. Espero que los siguientes contenidos puedan ayudarte en la práctica. Si tiene alguna pregunta, no dude en contactarnos.






A, B--- longitud de flexión de la pieza de trabajo
P'---coeficiente de flexión de la flexión del borde (factor de flexión: un factor menos una flexión)
R--- doblar y filetear (generalmente espesor de placa)
T--- espesor del material
La longitud expandida L=A+B-P', que es L=25+65-5,5=84,5
Según la Tabla 1, el espesor de la placa es 3, el troquel inferior es V25 y el coeficiente de flexión es 5,5.
Nota: Según la Tabla 1, los diferentes coeficientes de flexión de las matrices inferiores y los diferentes espesores de placa son diferentes.

A(A1), B--- longitud de flexión de la pieza de trabajo
P'---coeficiente de flexión de la flexión del borde (factor de flexión: un factor menos una flexión)
R--- doblar y filetear (generalmente espesor de placa)
T--- espesor del material
La longitud expandida L=A+T+B-2*P', que es L=50+2+50-2*3.4=95.2
Según la Tabla 1, el espesor de la placa es 2, el troquel inferior es V12 y el coeficiente de flexión es 3,4.
Nota: Según la Tabla 1, los diferentes coeficientes de flexión de las matrices inferiores y los diferentes espesores de placa son diferentes.

A(A1), B (B1): longitud de flexión de la pieza de trabajo
P'---coeficiente de flexión de la flexión del borde (factor de flexión: un factor menos una flexión)
R--- doblar y filetear (generalmente espesor de placa)
T--- espesor del material
La longitud expandida L=A+T+B+T-3*P', que es L=50+2+90+2-3*3.4=133.8
Según la Tabla 1, el espesor de la placa es 2, el troquel inferior es V12 y el coeficiente de flexión es 3,4.
Nota: Según la Tabla 1, los diferentes coeficientes de flexión de las matrices inferiores y los diferentes espesores de placa son diferentes.

A, B (B1): longitud de flexión de la pieza de trabajo
P'---coeficiente de flexión de la flexión del borde (factor de flexión: un factor menos una flexión)
R--- doblar y filetear (generalmente espesor de placa)
T--- espesor del material
La longitud expandida L=A+A+B+T+T-4*P', que es l = 25+25+100+1.5+1.5-4 * 2.8 = 141.8
Según la Tabla 1, el espesor de la placa es 1,5, el troquel inferior es V12 y el coeficiente de flexión es 2,8.
Nota: Según la Tabla 1, los diferentes coeficientes de flexión de las matrices inferiores y los diferentes espesores de placa son diferentes.

A(A1), B (B1): longitud de flexión de la pieza de trabajo
P'---coeficiente de flexión de la flexión del borde (factor de flexión: un factor menos una flexión)
R--- doblar y filetear (generalmente espesor de placa)
T--- espesor del material
La longitud de expansión L=A+T+A+T+B+B1+B1-6*P'
que es l = 50+1,5+50+1,5+150+20+20-6 * 2,8 = 276,2
Según la Tabla 1, el espesor de la placa es 1,5, el troquel inferior es V12 y el coeficiente de flexión es 2,8.
Nota: Según la Tabla 1, los diferentes coeficientes de flexión de las matrices inferiores y los diferentes espesores de placa son diferentes.

A, B--- longitud de flexión de la pieza de trabajo
P'---coeficiente de flexión del filete de aplanamiento
R--- doblar y filetear (generalmente espesor de placa)
T--- espesor del material
La longitud expandida L=A+B-P', que es L=25+65-1=89
Según la Tabla 2, el espesor de la placa es 2, el troquel inferior es V12 y el factor de flexión es la mitad del espesor de la placa.
Nota: Según la Tabla 2, la selección de diferentes troqueles inferiores tiene diferentes coeficientes de flexión y diferentes espesores de placa.
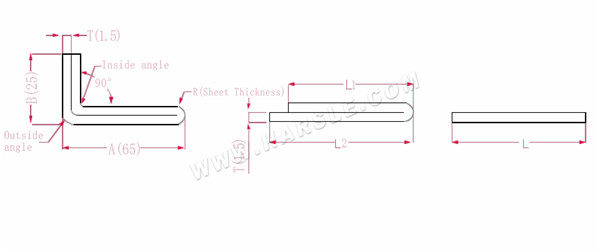
A, B--- longitud de flexión de la pieza de trabajo
P1--- coeficiente de flexión de la esquina interior
P2--- coeficiente de flexión del ángulo de flexión externo
R--- doblar y filetear (generalmente espesor de placa)
T--- espesor del material
La longitud expandida L1=(A-1.5) +(B-1.5)-P1, que es L1= (65-1.5) +(25-1.5)-3.2=83.8
L2=A+B-P2, que es L2=65+25-4.1=85.9
L=L1+L2-T/2, que es L=83,8+85,9-0,75=168,95
Según la Tabla 2, el espesor de la placa es 1,5, el troquel inferior es V12, el coeficiente de flexión de la esquina interior es 3,2, el coeficiente de flexión de la esquina exterior es 4,1 y el coeficiente de flexión 180 es 0,75.
Nota: Según la Tabla 2, los diferentes coeficientes de flexión de las matrices inferiores y los diferentes espesores de placa son diferentes.
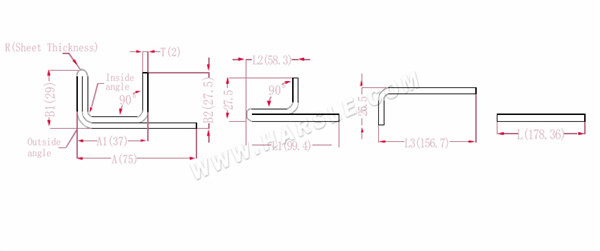
A, A1, A2, B1, B2, L, L1, L2, L3--- longitud de flexión de la pieza de trabajo
P1--- coeficiente de flexión de la esquina interior
P2--- coeficiente de flexión del ángulo de flexión externo
R--- doblar y filetear (generalmente espesor de placa)
T--- espesor del material
La longitud expandida L1=(A1-T) +(B2-T)-P1 que es L1= (35-2) +(34-2)-3.7=61.3
L2=(B1-T) +(A2-T)-P1, que es L2= (50-2) +(34-2)-3.7=76.3
L3=A+B1+B2-2*P2, que es L3=70+35+50-2*4.6+145.8
L=L1+L2+L3-2*P3, que es L=61,3+75,3+145,8-2*1=280,4
Según la Tabla 2, el espesor de la placa es 2, el troquel inferior es V12, el coeficiente de flexión de la esquina interior es 3,7, el coeficiente de flexión de la esquina exterior es 4,6 y el coeficiente de flexión de 90 es 1.
Nota: Según la Tabla 2, los diferentes coeficientes de flexión de las matrices inferiores y los diferentes espesores de placa son diferentes.
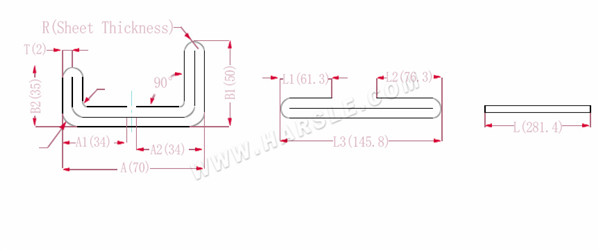
A, A1, A2, B1, B2, L, L1, L2, L3--- longitud de flexión de la pieza de trabajo
P1--- coeficiente de flexión de la esquina interior
P2--- coeficiente de flexión del ángulo de flexión externo
R--- doblar y filetear (generalmente espesor de placa)
T--- espesor del material
La longitud expandida L1=(A1-T) +(B2-T)-P1 que es L1= (35-2) +(34-2)-3.7=61.3
L2=(B1-T) +(A2-T)-P1, que es L2= (50-2) +(34-2)-3.7=76.3
L3=A+B1+B2-2*P2, que es L3=70+35+50-2*4.6+145.8
L=L1+L2+L3-2*P3, que es L=61,3+75,3+145,8-2*1=280,4
Según la Tabla 2, el espesor de la placa es 2, el troquel inferior es V12, el coeficiente de flexión de la esquina interior es 3,7, el coeficiente de flexión de la esquina exterior es 4,6 y el coeficiente de flexión de 90 es 1.
Nota: Según la Tabla 2, los diferentes coeficientes de flexión de las matrices inferiores y los diferentes espesores de placa son diferentes.
Diagrama y fórmula de cálculo de flexión escalonada.
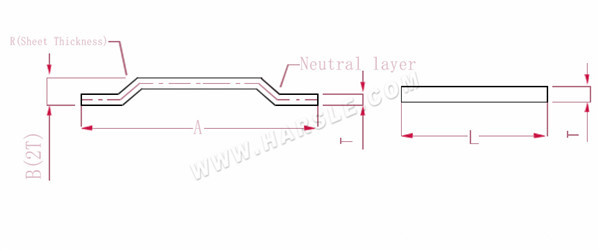
A, B--- longitud de flexión de la pieza de trabajo
R--- doblar y filetear (generalmente espesor de placa)
T--- espesor del material
Longitud desplegada L=A+1
Nota: Cuando el paso sea igual al espesor de dos placas, agregue 0,5 por cada paso y 1 por cada paso.
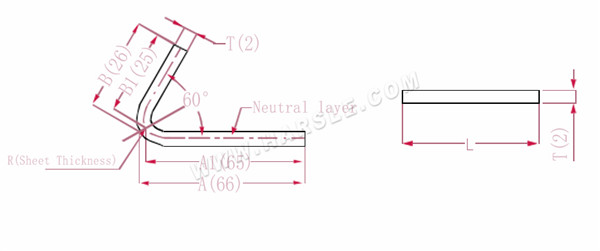
A(A1), B (B1): longitud de flexión de la pieza de trabajo
P'---coeficiente de flexión de la flexión del borde (factor de flexión: un factor menos una flexión)
R---doblar y filetear (generalmente espesor de placa)
T--- espesor del material
La longitud de expansión L=(AT) +(BT)-P', que es L= (66-1) +(26-1)-2=65+25-2=88
Según la Tabla 3, el espesor de la placa es 2, el troquel inferior es V12 y el coeficiente de flexión 60 es 2.
Nota: Según la Tabla 3, la capa neutra se selecciona como longitud y ancho de flexión.
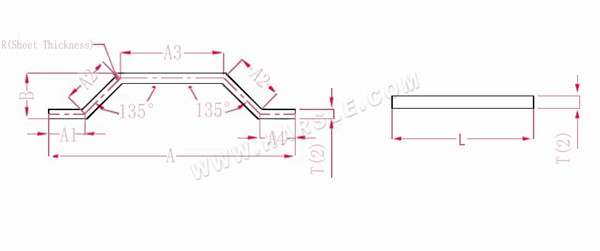
A (A1, A2, A3, A4), B--- longitud de flexión de la pieza de trabajo
P--- factor de flexión de 135 ángulos de flexión
R--- doblar y filetear (generalmente espesor de placa)
T--- espesor del material
La longitud de expansión L = A1+A2+A3+A2+A4-PP.
Nota: el mismo paso de presión de flexión solo necesita reducir dos coeficientes
Según la Tabla 3: el espesor de la placa es 2, el troquel inferior es V12 y el coeficiente de flexión en 135 es 1,1.
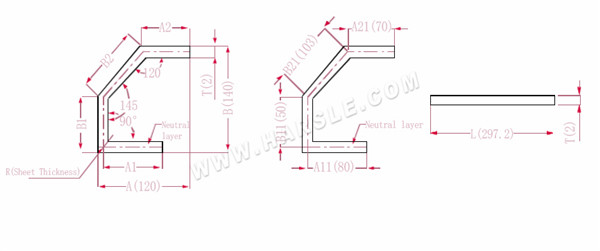
A (A1, A2), B (B1, B2): longitud de flexión de la pieza de trabajo
P1---coeficiente de flexión de 120°
P2---coeficiente de flexión de 145°
P3---coeficiente de flexión de 90°
R--- doblar y filetear (generalmente espesor de placa)
T--- espesor del material
Nota: si el tamaño del gráfico está marcado en la forma, el tamaño de la forma debe convertirse al tamaño de capa neutra al calcular la longitud de despliegue;
La longitud de expansión L=A11+B11+B21+A21-P1-P2-P3, que es l = 80+50+103+70-1.7-0.7-3.4 = 297.2
Según la Tabla 3: el espesor de la placa es 2, el troquel inferior es V12, el coeficiente de flexión 120 es 1,7, el coeficiente de flexión 145 es 0,7 y el coeficiente de flexión 90 es 3,4
Nota: Según la Tabla 3, los diferentes coeficientes de flexión de las matrices inferiores y los diferentes espesores de placa son diferentes.
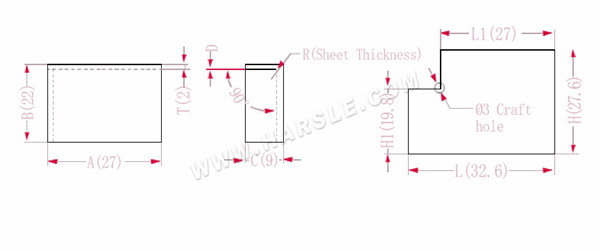
A, B, C--- largo, ancho y alto del borde de flexión de la pieza de trabajo
P--- coeficiente de flexión
R--- doblar y filetear (generalmente espesor de placa)
H(H1), l (L1): la longitud desplegada de cada lado
T--- espesor del material
D--- espacio libre del proceso de doblado (generalmente 0~0,5)
La longitud expandida L1=A, que es L1=27
L=A+CP, que es L=27+9-3.4=32.6
H1=BTD, que es H1=22-2-0,2=19,8. Nota: D es 0,2.
H=B+CP, que es H=22+9-3.4=27.6
Según la Tabla 1: el espesor de la placa es 2, el troquel inferior es V12 y el coeficiente de flexión es 3,4
Nota: Según la Tabla 1, los diferentes coeficientes de flexión de las matrices inferiores y los diferentes espesores de placa son diferentes.
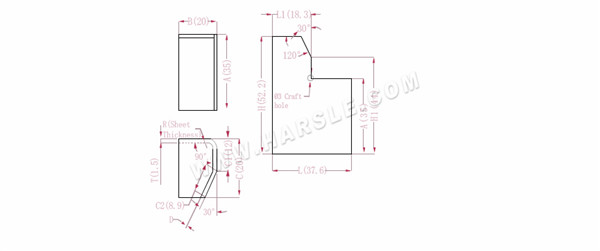
A, B, C--- largo, ancho y alto del borde de flexión de la pieza de trabajo
H(H1), L (L1): la longitud desplegada de cada lado
P---coeficiente de flexión de 90° P1---coeficiente de flexión de 30°
R--- doblar y filetear (generalmente espesor de placa)
T--- espesor del material
D--- espacio libre del proceso de doblado (generalmente 0~0,5)
La longitud expandida L1=BTD, que es L1=20-1,5-0,2=18,3
L=B+C1+C2-P-P1, que es L=20+12+8.9-2.8-0.5=37.6
H1=C1+APD, que es H1=12+35-2,8-0,2=44. Nota: D es 0,2.
H=A+CP, que es H=35+20-2.8=52.2
Según la Tabla 1: el espesor de la placa es 1,5, el troquel inferior es V12, el coeficiente de flexión es 2,8 y el coeficiente de flexión 30 es 0,5
Nota: Según la Tabla 1, los diferentes coeficientes de flexión de las matrices inferiores y los diferentes espesores de placa son diferentes.

A, B, C--- largo, ancho y alto del borde de flexión de la pieza de trabajo
H(H1), L (L1): la longitud desplegada de cada lado
P--- coeficiente de flexión
R--- doblar y filetear (generalmente espesor de placa)
T--- espesor del material
D--- espacio libre del proceso de doblado (generalmente 0~0,5)
La longitud expandida H1=B-B1-D, que es H1=50-12-0,3=37,7. Nota: D es 0,2.
H2=BTD que es H2=50-2,5-0,3=47,2
H=B+C+B1-2*P, que es H=50+47+12-2*4.5=100
L1=A+CTDP, que es L1=55+47-2,5-0,3-4,5=94,7
L=A+C+B2-2*P, que es L=55+47+12-2*4.5=105
Según Tabla 1: el espesor de la placa es 1,5, el troquel inferior es V16 y el coeficiente de flexión es 4,5
Nota: Según la Tabla 1, los diferentes coeficientes de flexión de las matrices inferiores y los diferentes espesores de placa son diferentes.